My research focuses on deriving and analyze theoretically and numerically new mathematical models that describe different multiscale processes in fluid mechanics.
The study of fluid behavior is essential for understanding various engineering phenomena and applications to other sciences, as it sheds light on the complex motion and interactions of liquids and gases. My research focuses on the study of different types of fluids:
Modeling non-Newtonian fluid flows in complex domains (such as thin domains, porous domains, rough domains, thin porous domains, or thin rough domains) is critical due to its practical applications, for example, in polymer processing, oil transportation in pipelines, hydrology, as well as food processing.

Thin porous media

Thin rough domains
The governing equations for the fluids I study are too complex to be solved in such domains due to their complex geometry. My research focuses on deriving macroscopic laws posed in simpler domains, containing averaged quantities that reflect domain heterogeneities, replacing the original physical laws and allowing us to approximate their behavior. To obtain these types of averaged equations, I improve and use recent techniques from Homogenization Theory.
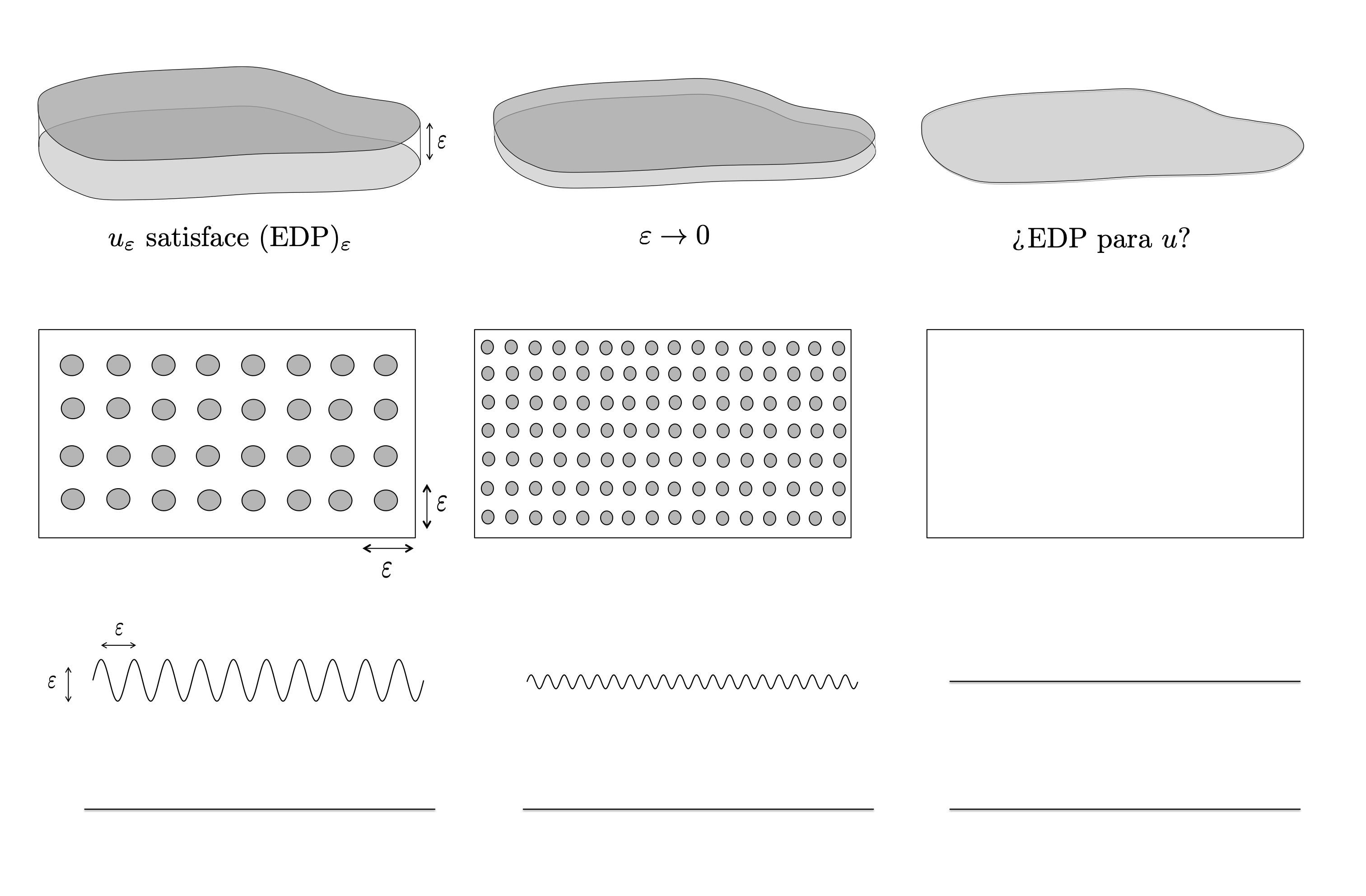
Homgenization process in thin, porous and rough domains
Once the macroscopic models have been obtained, they must be verified. Conventional numerical methods can be computationally very expensive to solve the original problems due to the complexity of the domain structures. However, the use of the resulting macroscopic models drastically reduces the computational cost of numerical resolution. To validate and compare the different models obtained, I perform numerical simulations, improving algorithms based on the Finite Element Method, for example, using the software FreeFem++.